Binary Search on Unsorted Arrays

Hello 👋! Welcome to this blog series on Data Structures and Algorithms, where we'll embark together on uncovering and understanding a wide range of data structures and algorithms available to solve problems.

In this post, we'll try to understand how Binary Search can be used to solve problems when the given input array is unsorted.

Prerequisites

Read and understand code
Basic understanding of Binary Search (fret not! There will be a recap of this too!)

This article is quite long and detailed. But I assure you that if you stick with me until the end, you will get a basic idea of when and how to apply binary search when the given input is not explicitly sorted.

Introduction

If you are here after reading the words Binary Search and Unsorted together and were fascinated, sorry to disappoint you, but it is not possible to use binary search on unsorted arrays/ lists! You've been click-baited!

What is possible is to try and come up with a sorted search space using the given constraints and input of a problem and try applying binary search if certain conditions are met.
How to come up with a sorted search space, and what are the conditions that allow you to use the binary search algorithm? You'll have to stick further to know that.

A Brief on Binary Search

Binary Search is a powerful algorithm which is primarily used for searching a target value in a sorted list.
To recap the idea, we maintain two pointers: low and high initially with low = 0 (assuming 0-based index) and high = n-1, where n is the number of elements in the list.
At every step, we find the middle element mid between the low and high pointers and compare the target with the value in mid.
Depending on the comparison, we eliminate one-half of the search space.
We repeat this comparison until the low pointer is less than or equal to the high pointer. If and when low > high, it means that the target was not present in the list.
The image below shows a sample implementation of the binary search algorithm:

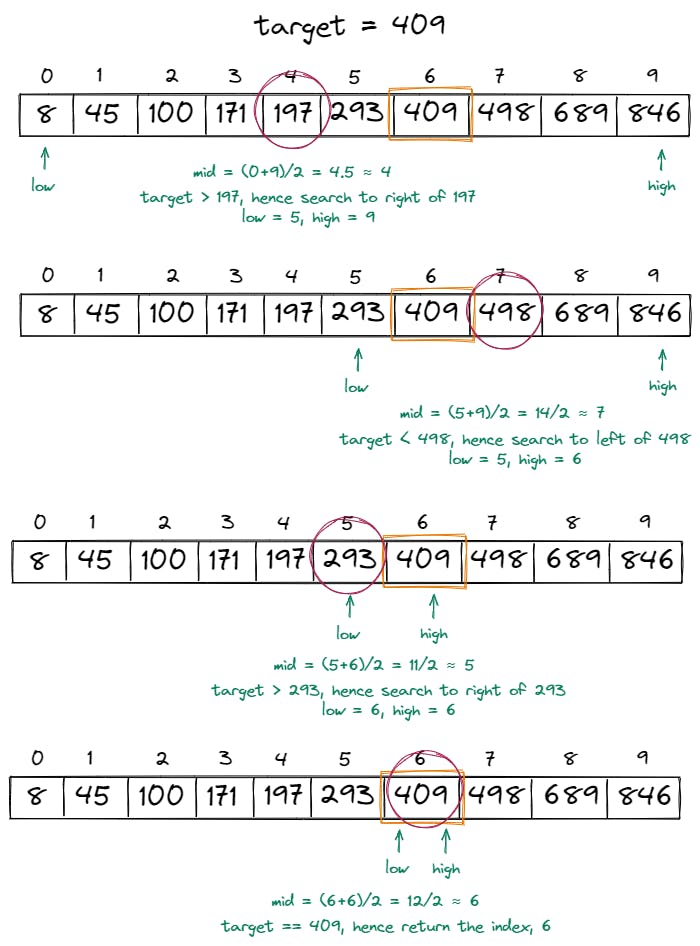
Below is the code for the algorithm:

  int binarySearch(int[] array, int target) {
      int n = array.length;
      int low = 0, high = n-1;
      while(low <= high) {
          int mid = low + (high - low)/2;

          if(array[mid] == target) return mid;

          if(array[mid] > target) {
              high = mid - 1;
          }
          else {
              low = mid + 1;
          }
      }
      return 
  }

The most vital part of the binary search implementation is eliminating the search space by one-half at every step.
- This elimination makes the algorithm fast and efficient. The rate of growth is slow for this algorithm. Even for large numbers, the process is quick.
  - Time complexity: O(log n), where n = the number of elements in the array.
- Let's say we had a dictionary with 1 million numbers and had to search for a word. In the worst case, we would only be making roughly 20 comparisons.
- Imagine using linear search -- we would have to make 1 million words in the worst case!!
Now that we've revised about binary, let's see how we can use the above binary search code and use it when our input is not explicitly sorted.

Predicate Functions

Before we get into how to use binary search when input is unsorted, let us review the example we saw in the previous section.
- The input array was: [8, 45, 100, 171, 197, 293, 409, 498, 689, 846].
When the middle element was at the index 4 during the first iteration, after comparison with the target 409, we saw that 197 > 409.
So at this step, we can visualize the above array after comparison as follows:
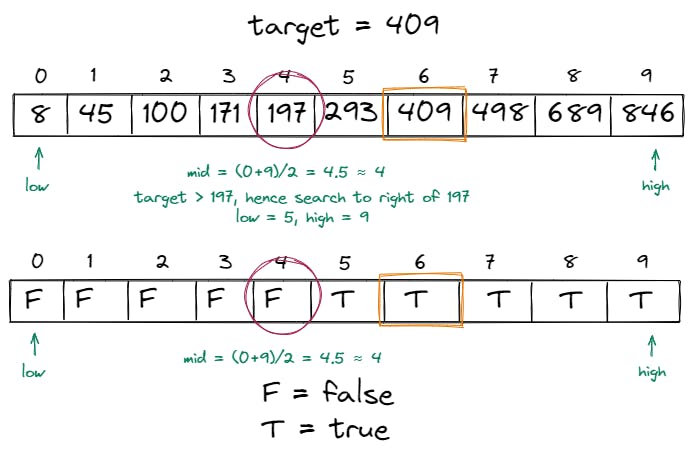
- Since the element in the middle is not equal to 409 and the list is sorted, it is guaranteed that the same comparison of array[mid] == target is always going to evaluate to false for every element before mid.
- Also, since 197 is not greater than 409 and the list is sorted, it is guaranteed that every element to the left of 197 is also not going to be greater than 409.
This comparison used in the binary search algorithm is a predicate.
Predicate is a function which results in either a true or false value (binary values).
- The comparison in the binary search- the middle element with the target results in either true or false.
- An example of a predicate function can be p(x) = x > 10. Any number less than or equal to 10 results in a false. But for every number from and after 11, the predicate will return true.
Further, the comparison we use for binary search is a monotonic predicate function.
- In binary search, we have a function p(x) to evaluate if the value in the middle is greater or less than the target. If p(x) = true for some x, then given the sorted property of the search space, it is a guarantee that p(y) should also be true for every y > x. Vice versa is also true.
- To put it simply, once the predicate for a value gives true, then the predicate for every value after it results in true as well.
- If any value evaluates to false, every value after it also results in false.
A monotonic predicate should always give results in the form T*F* or F*T*.
Hence, we can apply binary search to any such search space that results in a series of monotonic true or false when a predicate is applied.
Formally,

Binary search applies to any search space with a defined ordering, if there is a predicate such that p(x) implies p(y) for all y > x.

Example #1

Let's try to understand this concept of the predicate with a problem from Leetcode: First Bad Version. (Note that this problem involves input which is sorted. We will deal with unsorted inputs later).
- We are given a sorted search space consisting of versions of a product numbered [1...n] and we have to find the first bad version of the software.
- Any version developed after a bad version also leads to a buggy, bad product.
- The isBadVersion(version) API is given to us.
Let's see how to solve this problem. The ordering has already been given to us - the sorted list of products from [1...n].
As usual, we begin with the start and end pointers. Initially start = 1 and end = n.
Until the pointers start and end refer to the same bad version of the product, we will continue iterating and reducing our search space.
The next question is how do we reduce the search space?
- Because, unlike the usual binary search algorithm, we do not have a target to compare every element with.
- Hence, we'll have to find a predicate that will give us a monotonic result of T*F* or F*T* which will allow us to reduce the search space.
If you notice this line: each version is developed based on the previous version, all the versions after a bad version are also bad, you can see that here lies the idea for forming a predicate.
The API that's given to us is bool isBadVersion(version) and we have to keep reducing the search space using this.
The way we can do this is as follows:
- If a version is bad, then we know that every other version after that is bad. This could potentially also be the first bad version.
- If a version is good, then we know that every version before that was also good. We can ignore this version since we don't care about "good" versions.
In terms of pointers low, high, and mid where mid = low + (high - low)/2 if:
- isBadVersion(mid) == true all versions [mid+1...n] are going to be bad. Since this version could also be potentially the first bad, we will need to consider this as the endpoint for the next iteration. Hence update high = mid.
- isBadVersion(mid) == false all versions [1...mid] are going to be good. We don't care much about the good version so we can ignore the current version mid. So low = mid + 1.
After all the iterations, low == high, such that it will be the first bad version.
Let's use the sample test case: n = 5 and bad = 4 (of course, this bad version is what we'll have to find and it won't be given to us as arg in the function). We will iterate to find the bad version until low != high.
- low = 1, high=5, and mid = 3. isBadVersion(3) gives true. Now, we know that every version before 3 was also good. Hence, we can ignore the previous and current versions and shift low = mid+1 => 3+1 => 4.
- low = 4, high = 5 and mid = 4. isBadVersion(4) gives true. As this version is false, every version after it will also be false. Moreover, this could potentially be the first bad version. Hence, we'll assume this to be the end of the next iteration. high = mid => 4.
- low = 4, high = 4. Since low == high, the iteration ends here and we have found our first bad version.

The predicate in this problem is:

if isBadVersion(mid)

high = mid

else

low = mid + 1

Below is a pictorial representation of the steps we've taken:

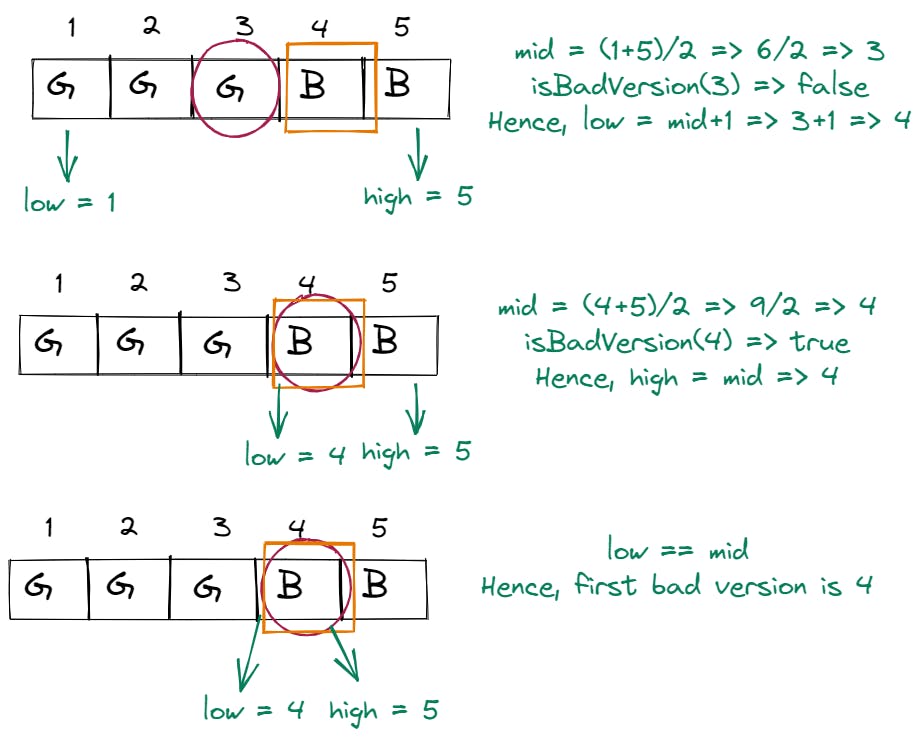
Below is the code for the above problem:

  /* The isBadVersion API is defined in the parent class VersionControl.
        boolean isBadVersion(int version); */

  public class Solution extends VersionControl {
      public int firstBadVersion(int n) {
          int low = 1, high = n;

          while(low < high) {
              // to avoid integer overflow
              int mid = low + (high - low)/2; 

              if(isBadVersion(mid)) {
                  high = mid;
              }
              else {
                  low = mid + 1;
              }
          }

          return low;
      }
  }

  Time Complexity: O(log n)
  Space Complexity: O(1)

Example #2

The previous question dealt with finding the first truth: truth here refers to the bad version.
Let's instead find the first bad version by finding the last good version, i.e. finding the last false rather than finding the first truth.
As before, we assume that we have the isBadVersion(num) API provided and we can use this to reduce the search space.
Now how do we reduce the search space? Let's look into both cases:
1. When the API isBadVersion(mid) returns false
  - This means that the given mid is a good version. Since this could potentially be the last good version, we will need to consider it for future iterations.
  - Hence low = mid.
2. When the API isBadVersion(mid) returns true
  - This means that the given mid was a bad version. Since we are concerned with the false values, we will ignore this version.
  - Hence high = mid - 1.
Now we know how to update our pointers and reduce our search space. But there is one edge case we've missed out on.
Let's revisit our earlier test case. But this time our input will be n = 5, bad = 5. Initially, low = 1, high = 5 and we will iterate and reduce search space until low != high.
- low = 1, high = 5 and mid = 3. isBadVersion(3) results in false. Hence, low = mid => 3.
- low = 3, high = 5 and mid = 4. isBadVersion(4) results in false. Hence, low = mid => 4.
- low = 4, high = 5 and mid = 4. isBadVersion(5) results in false. Hence low = mid => 4.
But wait, we had already reached the same state earlier!
When we try to update the value of low to mid to find the last falsy value, we will always be stuck in an infinite loop when the search space is finally down to 2 values: [x, y]. The x will always be chosen as the midpoint in this case.
To solve the infinite loop issue, we can update the calculation of mid as low + (high - low + 1)/2. This gives the ceiling value from the division rather than the floor.
The following image depicts the issue of the infinite loop where the element x1 is chosen as the mid over and over again when search space is down to [x1, x2]: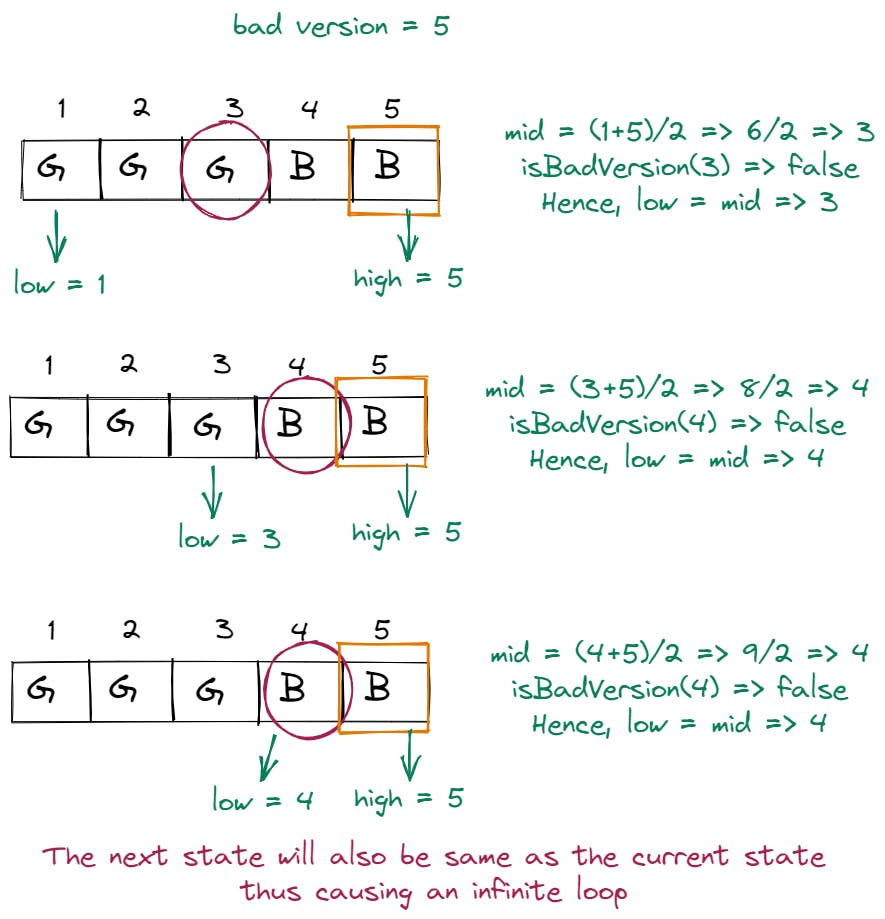

Below is the code for the above implementation where we find the last falsy and then use it to find the first bad version:

  /* The isBadVersion API is defined in the parent class VersionControl.
        boolean isBadVersion(int version); */

  public class Solution extends VersionControl {
      public int firstBadVersion(int n) {
          int low = 1, high = n;

          while(low < high) {
              // to avoid integer overflow
              int mid = low + (high - low + 1)/2; 

              if(isBadVersion(mid)) {
                  high = mid-1;
              }
              else {
                  low = mid;
              }
          }

          // when there are no good versions, then return the low itself
          if(low == 1 && isBadVersion(low)) return low;
          return low+1;
      }
  }

  Time Complexity: O(log n)
  Space Complexity: O(1)

Low mid and High mid

In short, there are two cases:
1. When we want the last false or the high mid, then we find the value of mid as:
```
 mid = low + (high - low + 1)/2
```
2. When we want the first truth or the low mid, then we update the value of mid as:
```
 mid = low + (high - low)/2
```

Example #3

We saw in the previous two examples the input was sorted. Now let's deal with unsorted input.
Let us solve the question to find the peak index in a mountain array.
- The input array given will be of a length greater than 3.
- Initially until a point, peak, increases and then decreases from there.
  - An e.g. is [0, 10, 5, 2] => The input increases until peaks at index 1 (value 10) and then decreases.
- Given the array, we need to find the index of the peak element.
The first step is to identify how we can form a predicate to move the pointers and reduce search space.
If you observe, the input can be split into two parts with one-half increasing [0..peak] and the other decreasing [peak+1...n-1].
Hence, we can form a relationship between the current element and the immediate element to its right.
We then have two cases:
1. The next element is greater than the current element
  - This is the increasing portion of the input. The peak element would lie in this portion.
2. The next element is smaller than the current element
  - The current element marks the end of the increasing portion and the current element could potentially be the peak element.
Hence, we can form a predicate such that we compare the current element mid with the next element mid+1.
If nums[mid] > nums[mid+1]: we move to the left side the mid could potentially be the peak index.
Else nums[mid] < nums[mid+1]: we move to the right side of the peak element.
Hence our predicate is this: nums[mid] > nums[mid+1].
Let's consider the following test case: [0, 10, 5, 2]. We will perform our algorithm until the pointers low and high remain unequal.
- low = 0, high = 3, and mid = 1.
  - nums[mid] > nums[mid+1] => 10 > 5 => true
  - Hence update high = mid => high = 1.
- low = 0, high = 1 and mid = 0.
  - nums[mid] > nums[mid+1] => 0 > 10 => false
  - Hence, update low = mid + 1 => low = 1.
- Finally, low = high = 1, hence we will stop the algorithm and return the index low (or high) as the peak index.

Below is the code for the problem:

  class Solution {
      public int peakIndexInMountainArray(int[] arr) {
          int n = arr.length;
          int low = 0, high = n-1;

          while(low < high) {
              int mid = low + (high - low)/2;

              // the peak could potentially be the mid element
              if(arr[mid] > arr[mid+1]) {
                  high = mid;
              }
              // increasing portion of array
              else {
                  low = mid + 1;
              }
          }

          return low;
      }
  }

  Time Complexity: O(log n)
  Space Complexity: O(1)

Example #4

Let us look at a final example to understand one of the main use cases of the modified binary search algorithm.
In this class of problems, the input will be unsorted. Along with the given constraints, we will have to use the input to obtain a sorted search space and then apply the modified algorithm.
The following problem from Interview Bit to allocate books is a good example. Let's use this to understand this class of problems.
- Given an array of N books, and an array A where A[i] represents the number of pages in the book i, our task is to allocate these pages to B (given) students such that the maximum number of pages allocated to a student is minimum.
- We are also given a few constraints:
  1. 1 book can be allocated to only 1 student
    - We cannot allocate say half the pages from the book i to student 1 and the other half to student 2.
  2. Each student should be allocated at least 1 book
    - If we have 4 students, then all 4 students must be allocated one book. We cannot say allocate all the available books to 1 student and allocate none to the remaining 3.
  3. Book i should be allocated before the book i+1
Let us review this sample test case: A = [12, 34, 67, 90], B = 2. We will have to allocate all these books to B students such that the maximum book allocated is the minimum.
Some possible ways include:
1. student 1: 12, student 2: 34, 67, 90
  - maximum pages allocated = 34 + 67 + 90 => 191
2. student 1: 12, 34, student 2: 67, 90
  - maximum pages allocated = 67 + 90 => 157
3. student 1: 12, 34, 67, student 2: 90
  - maximum pages allocated = 12 + 34 + 67 => 113
Out of all the three possible ways for the test case, 113 is the answer as the maximum number of pages allocated in this case is the least compared to 191 and 157.
To solve this problem, we will first have to figure out the search space.
For the time being, let's forget about the constraint to allocate B students and focus on the maximum number of pages that can be allocated.
1. The maximum number of pages allocated will be the least when we assign one book per student. In this case, the lowest maximum number of pages allocated will be the book which has the maximum number of pages defined as max(A).
2. The maximum number of pages that can be allocated will be the highest when we assign all the books to one student. In this case, the highest maximum number of pages allocated will be the sum of pages in all the books defined as sum(A).
Our search space is reduced to [max(A)...sum(A)] which is sorted
- Specifically, in this sample test case [90...203].
Now, in this search space, we will have to find the number of pages, say x (such that it's the least) so that they can be distributed to B students.
x should be such that every student must be allocated pages less than or equal to x.
If you notice, we have formed a mapping between the pages and student count.
Below is the graph that clearly describes this relationship
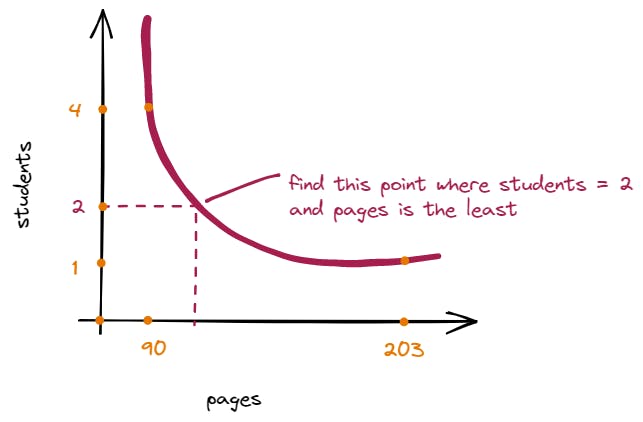
To find the least maximum pages to allocate to B students will use binary search on the search space.
- For every low and high value, we will set a barrier of the maximum number of pages that can be allocated per student defined as mid.
- We will then use this barrier mid to see how many students can be allocated the books such that the sum of pages per student is less than or equal to mid.
- If this barrier allows us to allocate pages to more than B students, then we must increase the value of this barrier to try and accommodate more books (leading to more pages) for a single student.
- If the barrier allows us to allocate pages to less than or equal to B students, then we must try to decrease the value of this barrier to accommodate fewer books (leading to fewer pages) for a single student.
Hence we can define a predicate canAllocate(barrier, B).
- canAllocate(barrier, B) == true, if the number of students allocated books is less than or equal to B.
- canAllocate(barrier, B) == false, if the number of students allocated books is more than B.

    if canAllocate(barrier, B):
        decrease the barrier
        this can be a potential least of the maximum
    else:
        increase the barrier to accommodate more books per student

More Formally, replacing barrier with mid:

  if canAllocate(mid, B):
      high = mid
  else:
      low = mid + 1

The below images show the process of using binary search to solve the sample test case: A = [12, 34, 67, 90] and B = 2
Hence, using binary search we will try to find the maximum pages per student that can be allocated using mid between intervals low and high.
Depending on whether or not it is possible to allocate all the books to the required number of students B, we will keep reducing the search space until low != high.
- This should be done such that every student has no more than the mid number of pages allocated.

Below is the code for the problem

  public class Solution {
      public int books(ArrayList<Integer> A, int B) {
          // It is impossible to allocate books to B students if
          // B > n (number of books)
          if(A.size() < B) return -1; 
          return binarySearch(A, B);
      }

      private int binarySearch(ArrayList<Integer> A, int B) {
          // the least maximum value is the max number of pages of all books
          // the highest maximum value is the total number of pages in all books
          int low = A.get(0), high = 0;

          for(int pages: A) {
              low = Math.max(pages, low);
              high += pages;
          }

          while(low < high) {
              int mid = low + (high - low)/2;

              if(canAllocate(mid, A, B)) {
                  high = mid;
              }
              else {
                  low = mid + 1;
              }
          }

          return low;
      }

      private boolean canAllocate(int pages, 
                  ArrayList<Integer> books, int students) {
          int total = 0, count = 1;

          // check how many students can be distributed books such that total pages <= pages
          for(int page: books) {
              if(total + page > pages) {
                  count++;
                  total = 0;
              }
              total += page;
          }

          return count <= students;
      }
  }

  Time Complexity: O(n * log n)
      - O(n) to try and allocate pages per student and get the count of students required
      - O(log n) to binary search in the search space [low,.. high]

Conclusion

Most of the problems with the binary search are not as straightforward as searching for a target in the search space. They would be similar to the problem solved in example#4.
Mostly you'll find the pattern of finding the least(first or highest of something in the search space. Similar to a greedy optimization problem where there is a defined ordering and constraints used to form a sorted search space.
This is the reason why there's a need for the modified algorithm which uses monotonic predicate functions.
The only issue with these sets of problems is identifying that they are binary search problems! This only comes with practice.
Hence, at the end of this article, I will be mentioning a Google doc that will contain a list of similar binary search problems that can help you to gain an in-depth understanding of identification, creation of search space and implementation of binary search.

Summary

Predicate is a function that returns binary values: either true or false.
Binary search can be used in problems where a predicate can be applied to any search space with a defined ordering and it results in either T*F* or F*T* pattern.
Usually in problems defined by endpoints low, high and the mid, we can either search for:
- low mid (first truth) defined by mid = low + (high - low)/2
- high mid (last false) defined by mid = low + (high - low + 1)/2

Resources

Thank you for reading this article on Binary Search. If you liked what I wrote and found this informative, please like, share and comment!

Special thanks and sincere gratitude to Deipayan Dash whose sessions helped to gain an in-depth understanding of solving problems with binary search on unsorted input using the predicate framework.