55. Jump Game

Hello, reader 👋🏽 ! Welcome to day 86 of the series on Problem Solving. Through this series, I aim to pick up at least one question every day and share my approach to solving it.

Today, I will be picking up LeetCode's daily challenge problem: 55. Jump Game.

🤔 Problem Statement

You are given an integer array nums. You are initially positioned at the array's first index, and each element in the array represents your maximum jump length at that position.
Return true if you can reach the last index, or false otherwise.
E.g.:
- nums = [2,3,1,1,4] => true
- nums = [3,2,1,0,4] => false

💬 Thought Process - Memoization (Possible TLE)

One of the ways to solve this problem is by trying out all the possibilities. Refer to the image below to understand what I mean:
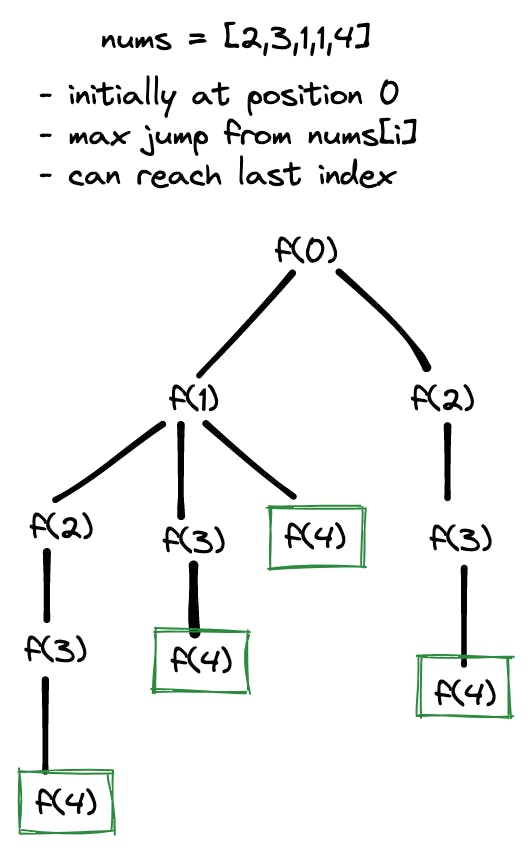
But trying out all the possible jumps would take O(n^n). If you see the above image, you can see that there are overlapping sub-problems.
Hence, we can cache using memoization and reduce the time complexity to O(n^2).
We can use an integer 1D array where if memo[index] = 1 means that from index we can reach the last element and memo[index] = 2 means that we cannot reach the last element.

Note: This approach sometimes leads to TLE so try it at your own risk!

👩🏽‍💻 Solution - Memoization (Possible TLE)

class Solution {
    private int[] memo;
    private int n;
    public boolean canJump(int[] nums) {
        n = nums.length;

        memo = new int[n];
        return canJumpHelper(nums, 0);
    }

    private boolean canJumpHelper(int[] nums, int index) {
        if(index >= n-1) {
            return true;
        }

        if(memo[index] != 0) {
            return (memo[index] == 1) ? true : false;
        }

        int jump = nums[index];

        for(int i = 1; i<=jump; i++) {
            boolean canReach = canJumpHelper(nums, index+i);
            if(canReach) {
                memo[index] = 1;
                return true;
            }
        }

        memo[index] = 2;
        return false;
    }
}

Time Complexity: O(n^2)
    - At every n calls, in the worst case O(n) work being done
Space Complexity: O(n)
    - Auxiliary space used for caching sub-problems

💬 Thought Process - Tabulation

We can use tabulation to convert the recursive, memoized solution to the tabulated approach.
This time, we can use a 1D boolean array where at any index, canReach[index] is true if from index we can reach the last element, else false.
We shall start iterating from the penultimate index and move on to the 0th index. This time as well for every index, we will cover an inner loop that would traverse and check all the possible jumps from index.
In the end if canReach[0] is true, then that means we were able to make jumps from the 0th index to the last index.

👩🏽‍💻 Solution - Tabulation

class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;

        /*
            If the max jump from 0th index is 0 and 
            number of elements is greater than 1, 
            then can never reach the last element
        */
        if(n > 1 && nums[0] == 0) {
            return false;
        }

        boolean[] canReach = new boolean[n];

        // can reach last element from last element
        canReach[n-1] = true; 

        for(int i = n-2; i >= 0; i--) {
            int maxJump = nums[i];
            int j = i+1;
            int lastJumpIndex = maxJump + i;

            while(j < n && j <= lastJumpIndex) {
                boolean canReachFromHere = canReach[j];
                if(canReachFromHere) {
                    canReach[i] = true;
                }
                j++;
            }
        }

        return canReach[0];
    }
}

Time Complexity: O(n^2)
    - At every n calls, in the worst case O(n) work being done
Space Complexity: O(n)
    - Auxiliary space used for caching sub-problems

💬 Thought Process - Greedy

There is a more efficient approach using greedy using which we can solve in O(n) time.
The idea is to traverse the elements from the end rather than from the start.
At every index, we would check if it's possible to cover the max jump and somehow reach the "target" index.
Initially, the target index is going to be the n-1 index. As we keep traversing, we'll check if we are able to jump at least till the target.
- If yes, then "target" is updated to the current index
- If not, then the "target" remains at the same index and we iterate backwards.
Once the loop ends, if the target is equal to the 0th index, that means we were able to make jumps from backwards and bring the "target" to the 0th index and return true. Else, return false.
- Refer to the image below to understand the solution better
- Below is another example for a case where the target would not shift if the jump is not possible

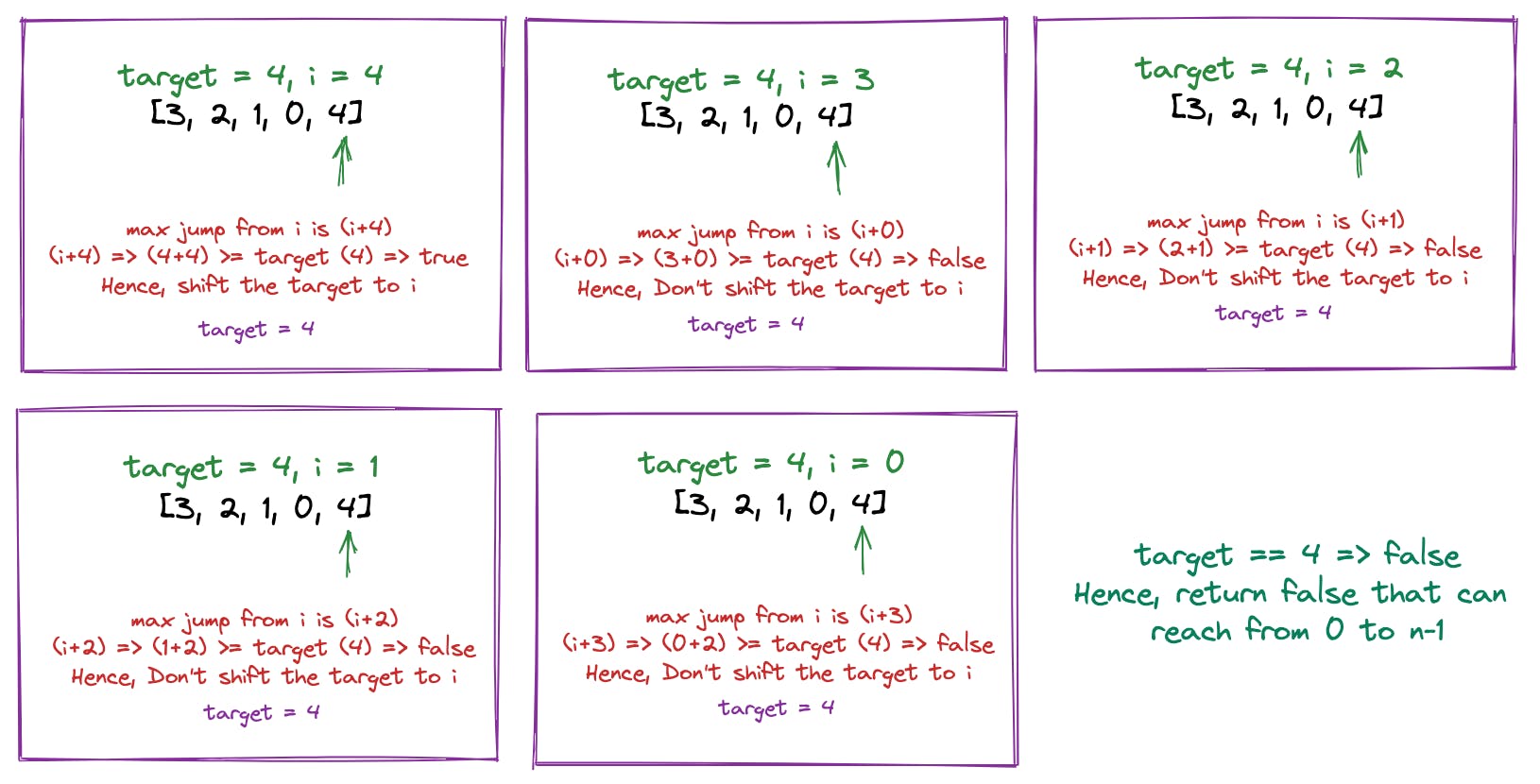
👩🏽‍💻 Solution - Greedy

class Solution {
    public boolean canJump(int[] nums) {
        int n = nums.length;

        int maxJump = nums[n-1];
        int target = n-1;
        int i = n-1;

        while(i >= 0) {
            int jump = nums[i];
            if(i + jump >= target) {
                target = i;
            }
            i--;
        }

        return target == 0;
    }
}

Time Complexity: O(n)
Space Complexity: O(1)

You can find the link to all the solutions on GitHub for this question here: 55. Jump Game.

Conclusion

That's a wrap for today's problem. If you liked my explanation then please do drop a like/ comment. Also, please correct me if I've made any mistakes or if you want me to improve something!

Thank you for reading!