790. Domino and Tromino Tiling

Hello, reader 👋🏽 ! Welcome to day 84 of the series on Problem Solving. Through this series, I aim to pick up at least one question every day and share my approach to solving it.

Today, I will be picking up LeetCode's daily challenge problem: 790. Domino and Tromino Tiling.

🤔 Problem Statement

• You have two types of tiles: a 2 x 1 domino shape and a tromino shape and they can be rotated.

• Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 10<sup>9</sup> + 7.

• In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

• E.g.:

  • n=1 => 1

  • n=3 => 5

💬 Thought Process - Brute Force

• This is a dynamic programming problem where we will have to try out all the possible ways of placing the given two tiles: domino and tromino, and return the total ways.

• But we do need to find out some way to represent and figure out ways to place tiles.

• Let's first focus on placing domino tiles. We'll take care of ways to place one tile both horizontally and vertically.

  • Look at the image below that places domino tile horizontally and vertically

![](https://cdn.hashnode.com/res/hashnode/image/upload/v1671893153761/af204523-75a5-4bae-a3a0-ea47553dc04b.png align="center")

Hence, placing a domino tile would have two options and our subproblem reduces to

f(n) = f(n-1) + f(n-2)

• What about tromino? Well tromino is the trickiest part.

• Before I explain ways to place tromino tiles, let's look at the possible orientations:

  

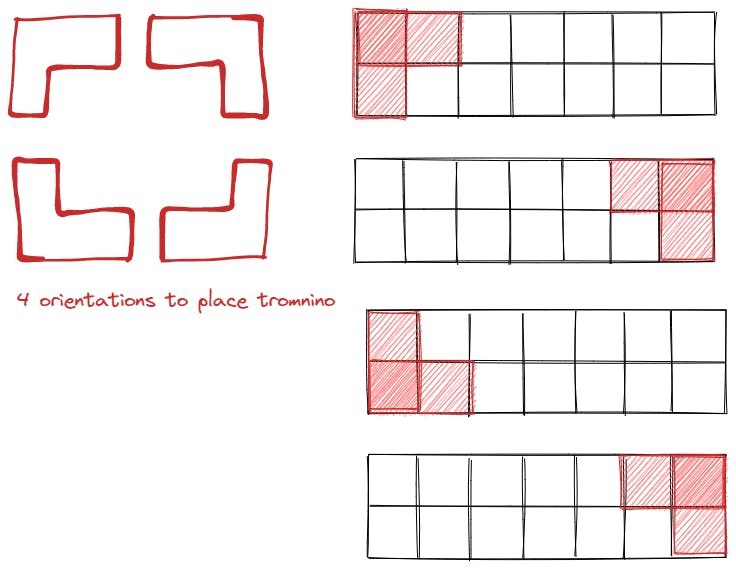
• Symmetrically, if we place trominoes in any of the above orientations the subproblems left to solve would be the same.

  • That is either the top or bottom row with an extra square

• Now that we have looked into the possible orientations, let's see the ways that we can actually place these tiles.

• Again, we'll try to place one tromino tile and look at the possible ways to fill the remaning board.

  

• We are done with the main function, but what of g(n)? We don't know how this is defined.

• Let's try to find how to define g(n) by building from the previous problem where we placed 1 tromino tile.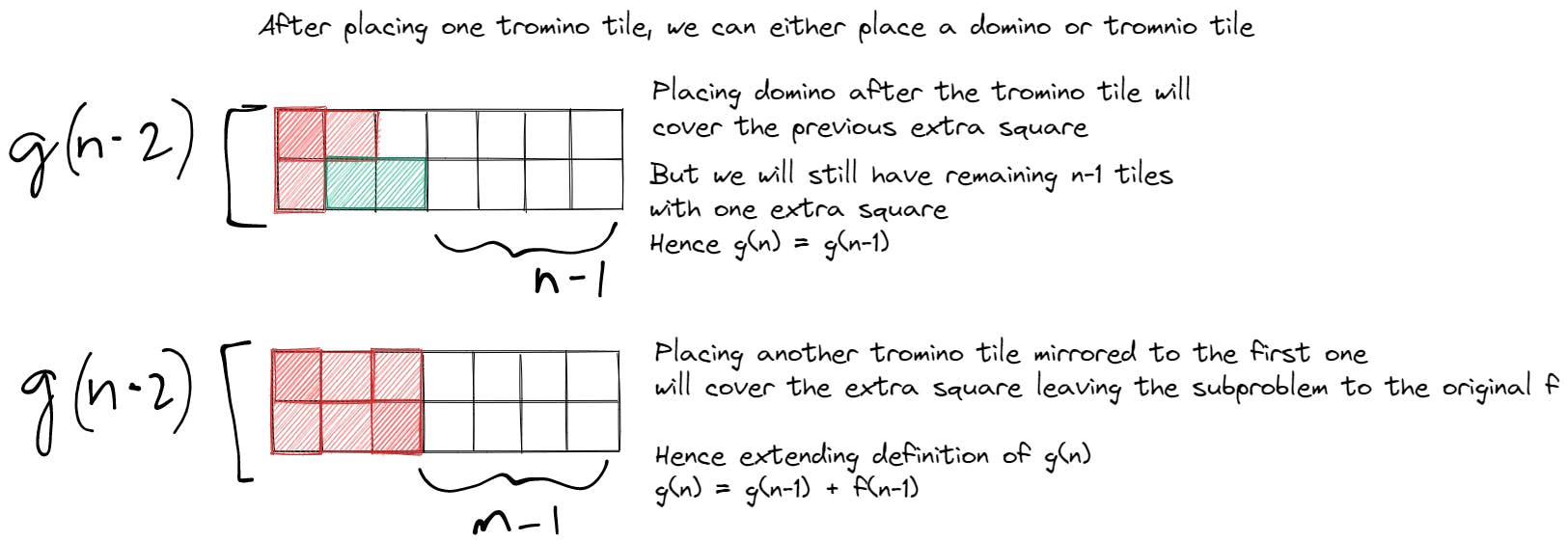

  

• Hence, our final equations boil down to this:

    f(n) = f(n-1) + f(n-2) + 2 * g(n-2)
    g(n) = f(n-1) + g(n-1)
  

• Now for the base cases:

  • for f the base cases would be:

    • f(0) the number of ways to tile are 0

    • f(1) the number of ways to tile are 1

    • f(2) the number of ways to tile are 2

  • for g the base cases would be:

    • g(0) the number of ways are 0

    • g(1) the number of ways are 1

      • Why? Well let's visualise how g(1) would look like on the board: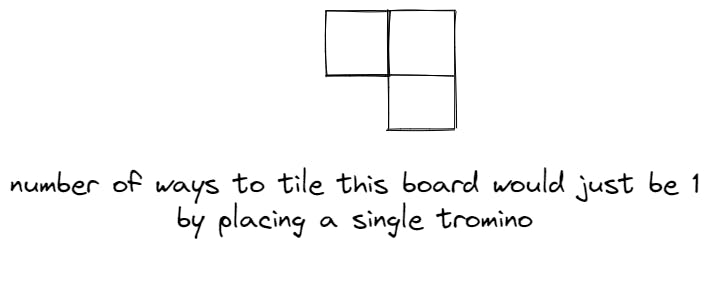

        

      • This is becasuse as stated earlier, g(n) would have columns in one row and the other row with n+1 columns.

• Hence, the final solution would be:

  ```java class Solution {

    int mod = (int) (1e9 + 7);
    public int numTilings(int n) {
        return (int) numTilingsHelper(n) % mod;
    }
  
    private long numTilingsHelper(int n) {
        if(n <= 0) return 0l;
        if(n <= 2) return n;
  

        // f(n-1) + f(n-2) + 2*g(n-2)
        long vert = numTilingsHelper(n-1) % mod;
        long hor = numTilingsHelper(n-2) % mod;
        long tro = numTilingsTromino(n-2) % mod;

        return (vert + hor + 2 * tro) % mod;
    }

    private long numTilingsTromino(int n) {
        if(n <= 0) return 0l;
        if(n == 1) return 1l;

        // g(n) = g(n-1) + f(n-1)
        long hor = numTilingsTromino(n-1) % mod;
        long tro = numTilingsHelper(n-1) % mod;

        return (hor + tro) % mod;
    }
}
```

• Now, we cannot simply use this as the final solution because we have multiple sub problems. The worst time complexity would be O(3^N).

• We can do better and it's not very diffiult to see that there are going to be subproblems.

• Also note how we are using long instead of int here as return values. This is necessary since we could be dealing with numbers outside of int range.

💬 Thought Process - Memoization

• There is only one dependent state: n. But we would require two different arrays to cache values. One to solve and cache sub-problems for f(n) and the other to cache and solve sub-problems for g(n).

👩🏽‍💻 Solution - Memoization

class Solution {
    int mod = (int) (1e9 + 7);
    long[] memo, tromino;
    public int numTilings(int n) {
        memo = new long[n+1];
        tromino = new long[n+1];

        Arrays.fill(memo, -1);
        Arrays.fill(tromino, -1);

        return (int) numTilingsHelper(n) % mod;
    }

    private long numTilingsHelper(int n) {
        if(n <= 0) return 0l;
        if(n <= 2) return n;

        if(memo[n] != -1) return memo[n] % mod;

        // f(n-1) + f(n-2) + 2*g(n-2)
        long verticalTile = numTilingsHelper(n-1) % mod;
        long horizontalTile = numTilingsHelper(n-2) % mod;
        long trominoTile = numTilingsTromino(n-2) % mod;

        return memo[n] = (verticalTile + horizontalTile + 
                          2 * trominoTile) % mod;
    }

    private long numTilingsTromino(int n) {
        if(n <= 0) return 0l;
        if(n == 1) return 1l;

        if(tromino[n] != -1) return tromino[n];

        // g(n) = g(n-1) + f(n-1)
        long horizontalTile = numTilingsTromino(n-1) % mod;
        long trominoTile = numTilingsHelper(n-1) % mod;

        return tromino[n] = (horizontalTile + trominoTile) % mod;
    }
}

Time Complexity: O(n)
Space Complexity: O(n)

💬 Thought Process - Tabulation

• We can convert the above solution to tabulation. Instead of recursive calls, we can use loops to calculate for the current value of n using previous solved sub-problems.

👩🏽‍💻 Solution - Tabulation

class Solution {
    int mod = (int) (1e9 + 7);
    public int numTilings(int n) {
        if(n == 0) return 0;
        if(n <= 2) return n;

        long[] dp = new long[n+1];
        long[] tromino = new long[n+1];
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 2;
        tromino[0] = 0;
        tromino[1] = 1;
        tromino[2] = 2;

        for(int i = 3; i<=n; i++) {
            dp[i] = (dp[i-1] + dp[i-2] + 2 * tromino[i-2]) % mod;
            tromino[i] = (tromino[i-1] + dp[i-1]) % mod;
        }

        return (int) dp[n];
    }
}

Time Complexity: O(n)
Space Complexity: O(n)

💬 Thought Process - Space Optimization

• We need only the answers to the two previous sub-problem for f(i) and one previous sub-problem for g(i).

• Hence we can use variables and keep updating them instead of using an entire array.

• We'll call the previous two states of the main sub-problem f() as firstTiling and secondTiling.

• For the tromino tiling sub-problem, let's call the first and second state as firstTromino and secondTromino.

• Each time we solve a sub-problem, we'll update firstTiling to the value of secondTiling and secondTilingto the value of the current answer of sub-problem.

• Similarly, each time we solve a sub-problem for the tromino tiling case, we'll update firstTromino to the value of secondTromino and the secondTromino to the value of the current answer of sub-problem.

• Finally, we can return the answer in the secondTiling variable.

👩🏽‍💻 Solution - Space Optimization

class Solution {
    int mod = (int) (1e9 + 7);
    public int numTilings(int n) {
        if(n == 0) return 0;
        if(n <= 2) return n;

        long firstTiling = 1;
        long secondTiling = 2;

        long firstTromino = 1;
        long secondTromino = 2;

        for(int i = 3; i<=n; i++) {
            long currentTiling = (firstTiling + secondTiling + 
                                  2 * firstTromino) % mod;
            long currentTromino = (secondTromino + secondTiling) % mod;

            firstTiling = secondTiling;
            secondTiling = currentTiling;

            firstTromino = secondTromino;
            secondTromino = currentTromino;
        }

        return (int) secondTiling;
    }
}

Time Complexity: O(n)
Space Complexity: O(n)

💬 Thought Process - Breaking down the equation

• So far, our equations are as follows:

    f(n) = f(n-1) + f(n-2) + 2 * g(n-2) --- #1
    g(n) = f(n-1) + g(n-1) --- #2
  

• Turns out, this could further be shortened to avoid the extra g(n) variable function.

• We'll understand how this works.

• Before that let's see what the value of g(n-2) would be:

    g(n-2) = f(n-3) + g(n-3)
  

• Using the above equation in the #1 we get:

    f(n) = f(n-1) + f(n-2) + f(n-3) + g(n-3) + f(n-3) + g(n-3)
  

• This can be regrouped as:

    f(n) = f(n-1) + f(n-3) + [f(n-2) + f(n-3) + g(n-3) + g(n-3)]
  

• The equation: f(n-2) + f(n-3) + g(n-3) + g(n-3) is basically the value of f(n-1)

• Hence, we arrive at:

    f(n) = f(n-1) + f(n-3) + f(n-1)
    f(n) = 2 * f(n-1) + f(n-3)
  

• Hence, we'll use three variables: firstTiling, secondTiling and thirdTiling. Initially, firstTiling will be equal to f(1) => 1, secondTiling will be equal to f(2) => 2, and thirdTiling will be equal to f(3) => 5.

• We'll loop from n=4 to calculate future sub-probllems and finally return the value in thirdTiling.

👩🏽‍💻 Solution - Breaking down the equation

class Solution {
    int mod = (int) (1e9 + 7);
    public int numTilings(int n) {
        if(n == 0) return 0;
        if(n <= 2) return n;

        long firstTiling = 1; // f(1) 
        long secondTiling = 2; // f(2)
        long thirdTiling = 5; // f(3)


        for(int i = 4; i<=n; i++) {
            // 2 * n-1 + n-3
            long currentTiling = ((2 * thirdTiling) + firstTiling) % mod;
            firstTiling = secondTiling;
            secondTiling = thirdTiling;
            thirdTiling = currentTiling;
        }

        return (int) thirdTiling;
    }
}

Time Complexity: O(n)
Space Complexity: O(n)

• You can find the link to all the four solutions on the GitHub for this question here: 790. Domino and Tromino Tiling.

Conclusion

That's a wrap for today's problem. If you liked my explanation then please do drop a like/ comment. Also, please correct me if I've made any mistakes or if you want me to improve something!

Thank you for reading!