834. Sum of Distances in Tree

Hello, reader 👋🏽 ! Welcome to day 82 of the series on Problem Solving. Through this series, I aim to pick up at least one question every day and share my approach to solving it.

Today, I will be picking up LeetCode's daily challenge problem: 834. Sum of Distances in Tree.

🤔 Problem Statement

There is an undirected connected tree with n nodes labelled from 0 to n - 1 and n - 1 edges.
You are given the integer n and the array edges where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
Return an array answer of length n where answer[i] is the sum of the distances between the ith node in the tree and all other nodes.

E.g.:

n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
=> [8,12,6,10,10,10]
n = 1, edges = []
=> [0]
n = 2, edges = [[1,0]]
=> [1,1]

💬 Thought Process - Naive

This hard tag on this problem is appropriate. This problem is essentially DP on trees, but before stating why, we need to understand the naive approach.
The problem is that we need to find the sum of distances (read depth) from every node to every other node.
Let's take the root node, in the below example:
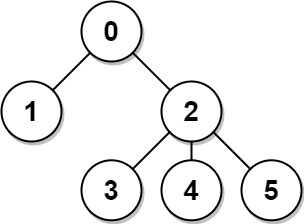
From node with value 0, 1 and 2 are at distances 1. Nodes 3, 4, 5 are all at distances 2 from 0.
This can be done by rooting all the other nodes and calculating the distance. Note that this takes O(n^2).
Can we do better? Yes, with Dynamic Programming, this problem can be solved in O(n).
What we can think is that when we keep trying to root the tree at different nodes, some count of nodes get closer while others get farther.
For e.g., if the tree is rooted at 2, the nodes 1, 3, 4, 5 get closer while 1 moves further.
- Similarly, if rooted at the node 3, node 2 is closed while the other nodes get further.
The key is, if we know the count of nodes that have gone farther or closer as well as the sum of distances from all those nodes, we can easily find the sum of distances rooted at every node.
Thus, we will have to do preprocessing steps to find the number of nodes that become closer and farther as well as the sum of distances of subtree at every node.

💬 Thought Process - Dynamic Programming

We will have to do two preprocessing steps: count the number of nodes from rooted at the subtree node, and the sum of the distances of every child from node.
If we only consider the root node of the tree, then the result is: sum of distances in left subtree + number of nodes in left subtree + sum of distances in right subtree + number of nodes in the right subtree.

Why do we need to consider the number of nodes at any subtree rooted at node? This is because the nodes in any subtree (including node) will be one more edge away from the parent of node compared to from node.

Below is the code to figure out how to do the count of nodes as well as the distance sum at any tree.

void getCountAndResultAtSubtrees(int root, int parent) {
    for(int child: adjList.get(root)) {
        // if the child is same as parent 
        // continue to avoid cycle
        if(child == parent) continue;
        getCountAndResultAtSubtrees(child, root);
        countNodes[root] += countNodes[child];
        distanceSum[root]] += distanceSum[child] + 
                              countNoded[child]
    }

    // increment the count of the current subtree 
    // to include parent
    countNodes[root]++;
}

The below image summarizes the above code:

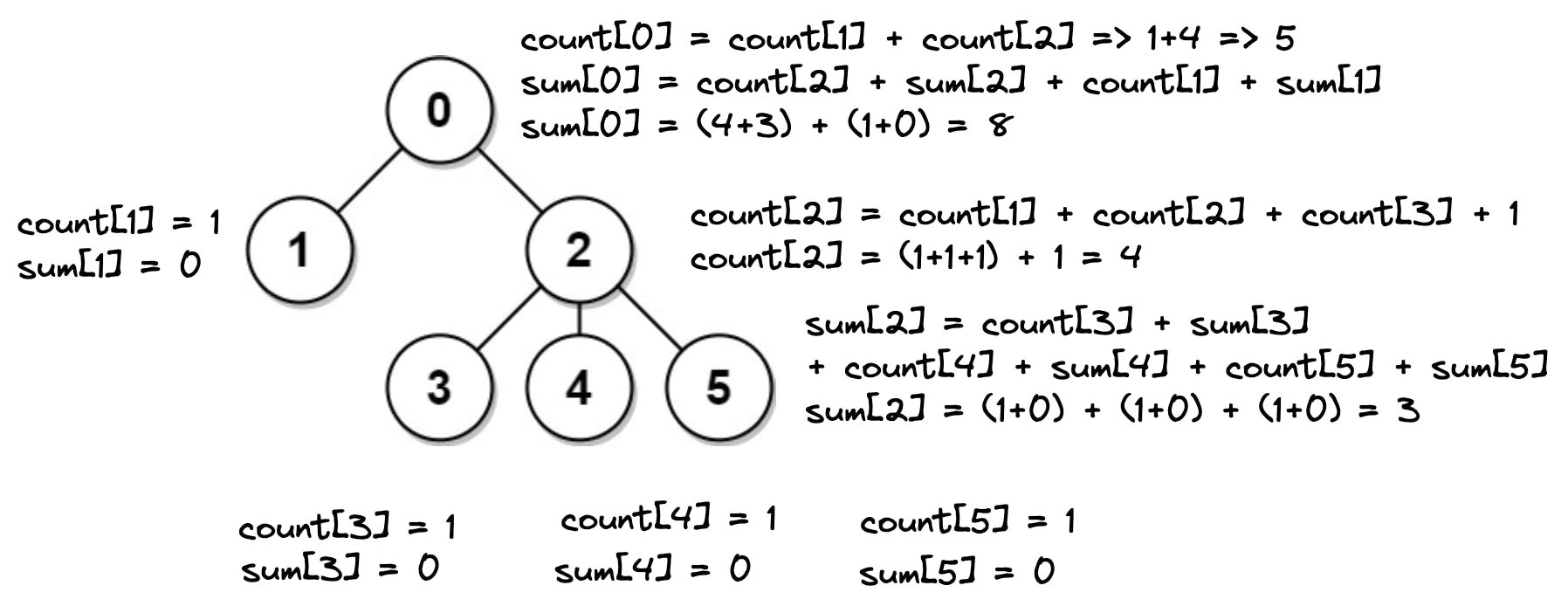
Now that we have calculated the initial step, we need to somehow make use of this information to get the final answer.
We will try to use the pre-processed info by trying to root every node and find the sum of distances.
Let us consider the case when 2 becomes the root and we need to find the sum of distances from 2 to every other node.
- count[2] number of nodes gets 1 unit closer to 2 now and n - count[2] number of nodes gets 1 unit away from 2.
- We can use the sum of distances from the root node to calculate this answer.
  - sum[2] = sum[0] - count[2] + n - count[2]
  - In our case, sum[2] = 8 - 4 + 6 - 4 -> sum[2] = 4+2 -> sum[2] = 6.

This solution is not pretty straightforward and intuitive. But if you try dry running the code on multiple graph instances, you'll begin to see the reasons behind the algorithm.

👩🏽‍💻 Solution - Dynamic Programming

Below is the code for the approach for solving this problem using dynamic programming on trees.

class Solution {
    private List<HashSet<Integer>> adj;
    private int[] countNodes;
    private int[] sumDist;

    public int[] sumOfDistancesInTree(int n, int[][] edges) {
        // generate adjacency list
        adj = new ArrayList();
        for(int i = 0; i<n; i++) {
            adj.add(new HashSet());
        }
        generateAdjList(edges, n);

        countNodes = new int[n];
        sumDist = new int[n];

        getDistFromRoot(0, -1);
        getSumOfDistances(0, -1, n);
        return sumDist;
    }

    private void generateAdjList(int[][] edges, int n) {
        for(int[] edge: edges) {
            int u = edge[0], v = edge[1];
            adj.get(u).add(v);
            adj.get(v).add(u);
        }
    }

    private void getDistFromRoot(int root, int parent) {
        for(int child: adj.get(root)) {
            if(child == parent) continue;

            getDistFromRoot(child, root);

            countNodes[root] += countNodes[child];
            sumDist[root] += sumDist[child] + countNodes[child];
        }

        countNodes[root]++;
    }

    private void getSumOfDistances(int root, int parent, int n) {
        for(int child: adj.get(root)) {
            if(child == parent) continue;

            sumDist[child] = sumDist[root] - countNodes[child] + n - countNodes[child];
            getSumOfDistances(child, root, n);
        }
    }
}

Time Complexity: O(n)
Space Complexity: O(n)

You can find the link to the GitHub repo for this question here: 834. Sum of Distances in Tree.

Conclusion

That's a wrap for today's problem. If you liked my explanation then please do drop a like/ comment. Also, please correct me if I've made any mistakes or if you want me to improve something!

Thank you for reading!